Hello everyone,
I'd like to introduce you all to a project that I've been working on with our lovely mod and resident statistical mathematician QxC4eva designed to improve the BSR Calculator and subsequently stats stages. This is a direct response to G-Luke's post about The Over Tuning of CAP Creations as found here, and the specific issue of inflated BSTs and highly optimised offensive dump stats. As has been mentioned in this thread, as well as the thread for the BSR itself, part of the reason for this bias is in the way that BSR is calculated as a summation of all of the individual values. Subsequently, an easy way to slide into the BSR limits for Stat stages is to dump either Attack or Sp. Atk as a means to bring down the PS and SS values enough to fit within the limits.
For those that were involved in the Stats Stages for our most recent process, CAP 28, you will remember that as TL for stats I attempted to address this problem of dumping the unused offensive stat through the use of a PS or SS mask that required the manual input of a specific PS or SS value into its respective column in the calculator to override its real value, as a means to address the way that BSR was calculated. While I think that this was suitable for the needs of that specific project as a quick, band-aid solution to address the possibility of having Mixed, as well as purely Physical or Special submissions, as seen in the diversity of submissions and slated options, choosing the specific numerical value for the mask was quite challenging due to there being little frame of reference. With this in mind, I have been interested in finding a more permanent solution to this problem.
While there have been a few different drafts that I've gone through, in the interests of brevity, I will be focusing only on what I view as the current optimal version of the BSR calculator. To summarise, I have added a new Stat Bias column to be accounted for when calculating the BSR. I have provisionally named this stat bias OSD standing for 'Offensive Stat Differential,' which is, as implied by its name and in line with the other stat biases, the standardised absolute value between a Pokemon's PS and SS values. Before I continue to explain how this works in practice, I just wanted to mention that it was quziel that first gave me the idea to include a modifier to BSR based around a Pokemon's PS and SS differential, and as such would like to thank them for the inspiration.
As part of this broader project, QxC4eva has also moved the BSR calculator spreadsheet to Google Sheets and automated the process of determining values and adding new Pokemon to the calculator which is fantastic. As such, rather than having to edit a constant to change the BSR, now all that is needed is to change the Standard Deviation values of the individual Stat Bias and BSR columns. This has allowed for finding what I consider to be an ideal OSD weighting of 22 SD that I believe In removes the disproportionate bias that the current BSR calculator has against Pokemon with two high offensive stats by better accounting for the fact that most offensive Pokemon will benefit from one high attack stat at a time, while still maintaining the principle that increasing the dump stat of PS or SS will also raise the BSR. That being said, under the new spreadsheet it is very easy to modify should that be required. OSD is designed to be a value that does not to be stipulated by the TL, but instead to allow for a diversity of spreads, either Mixed, Physical or Special, to all hit the necessary benchmarks and parameters that a TL may set.
To see how this change works in practice, I've included a comparison of the Top 20 CAP Metagame Pokemon by Usage (according to September 2020) below.
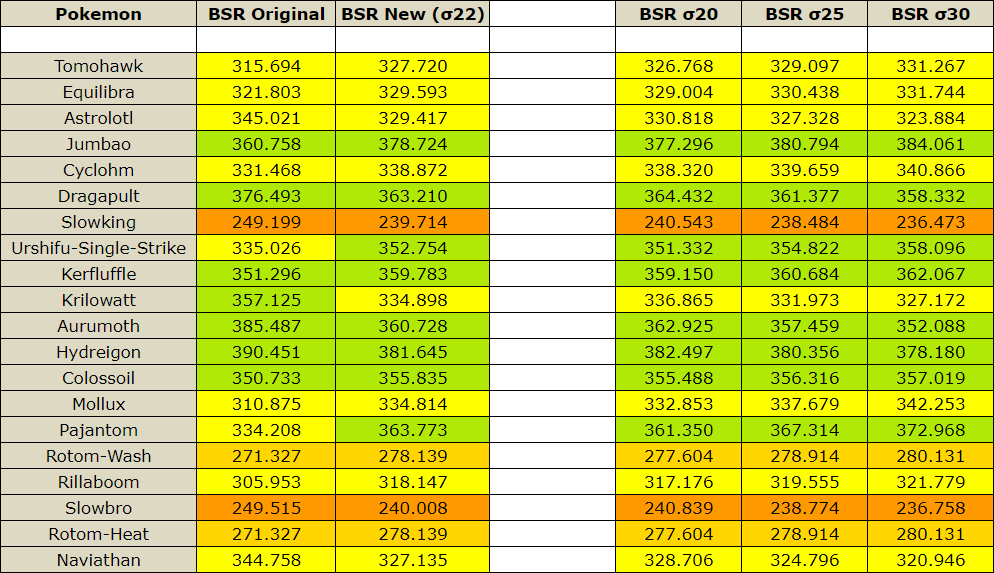
As is clear from the diagram, we can see that many mixed attackers have seen their BSR values go down fairly dramatically such as Krilowatt, Naviathan and Aurumoth, while many pure Physical or Special attackers such as Urshifu and Pajantom have seen their BSR values go up by quite a bit to reflect their dump stats. In addition it should also be clear from the later 3 columns to see how changing the SD value of OSD can have a pretty drastic effect. Changing the SD to 0 actually restores the original BSR calculation. Having discussed with a few people on discord, a value in between 20 and 25 was ideal, and as such why I decided on 22.
To demonstrate why I think this is an effective change for future stat processes, I will now compare a few different working spreads and how their values change as stats go up and down in both the old BSR and the new BSR in relation to the parameters that a TL may set, as well as discuss how the most recent slate of stat options for CAP 28 would have changed.
I realise that this is a massive wall of text, and I hope it hasn't been too daunting to get through. To anyone that wants to have a play with the updated calculator you can find a link to it here, just make sure to make your own copy to edit. I would love to hear all of your thoughts about these changes and the spreadsheet itself. With any luck this will be fully operational for CAP 29.
I'd like to introduce you all to a project that I've been working on with our lovely mod and resident statistical mathematician QxC4eva designed to improve the BSR Calculator and subsequently stats stages. This is a direct response to G-Luke's post about The Over Tuning of CAP Creations as found here, and the specific issue of inflated BSTs and highly optimised offensive dump stats. As has been mentioned in this thread, as well as the thread for the BSR itself, part of the reason for this bias is in the way that BSR is calculated as a summation of all of the individual values. Subsequently, an easy way to slide into the BSR limits for Stat stages is to dump either Attack or Sp. Atk as a means to bring down the PS and SS values enough to fit within the limits.
For those that were involved in the Stats Stages for our most recent process, CAP 28, you will remember that as TL for stats I attempted to address this problem of dumping the unused offensive stat through the use of a PS or SS mask that required the manual input of a specific PS or SS value into its respective column in the calculator to override its real value, as a means to address the way that BSR was calculated. While I think that this was suitable for the needs of that specific project as a quick, band-aid solution to address the possibility of having Mixed, as well as purely Physical or Special submissions, as seen in the diversity of submissions and slated options, choosing the specific numerical value for the mask was quite challenging due to there being little frame of reference. With this in mind, I have been interested in finding a more permanent solution to this problem.
While there have been a few different drafts that I've gone through, in the interests of brevity, I will be focusing only on what I view as the current optimal version of the BSR calculator. To summarise, I have added a new Stat Bias column to be accounted for when calculating the BSR. I have provisionally named this stat bias OSD standing for 'Offensive Stat Differential,' which is, as implied by its name and in line with the other stat biases, the standardised absolute value between a Pokemon's PS and SS values. Before I continue to explain how this works in practice, I just wanted to mention that it was quziel that first gave me the idea to include a modifier to BSR based around a Pokemon's PS and SS differential, and as such would like to thank them for the inspiration.
As part of this broader project, QxC4eva has also moved the BSR calculator spreadsheet to Google Sheets and automated the process of determining values and adding new Pokemon to the calculator which is fantastic. As such, rather than having to edit a constant to change the BSR, now all that is needed is to change the Standard Deviation values of the individual Stat Bias and BSR columns. This has allowed for finding what I consider to be an ideal OSD weighting of 22 SD that I believe In removes the disproportionate bias that the current BSR calculator has against Pokemon with two high offensive stats by better accounting for the fact that most offensive Pokemon will benefit from one high attack stat at a time, while still maintaining the principle that increasing the dump stat of PS or SS will also raise the BSR. That being said, under the new spreadsheet it is very easy to modify should that be required. OSD is designed to be a value that does not to be stipulated by the TL, but instead to allow for a diversity of spreads, either Mixed, Physical or Special, to all hit the necessary benchmarks and parameters that a TL may set.
To see how this change works in practice, I've included a comparison of the Top 20 CAP Metagame Pokemon by Usage (according to September 2020) below.
As is clear from the diagram, we can see that many mixed attackers have seen their BSR values go down fairly dramatically such as Krilowatt, Naviathan and Aurumoth, while many pure Physical or Special attackers such as Urshifu and Pajantom have seen their BSR values go up by quite a bit to reflect their dump stats. In addition it should also be clear from the later 3 columns to see how changing the SD value of OSD can have a pretty drastic effect. Changing the SD to 0 actually restores the original BSR calculation. Having discussed with a few people on discord, a value in between 20 and 25 was ideal, and as such why I decided on 22.
To demonstrate why I think this is an effective change for future stat processes, I will now compare a few different working spreads and how their values change as stats go up and down in both the old BSR and the new BSR in relation to the parameters that a TL may set, as well as discuss how the most recent slate of stat options for CAP 28 would have changed.
Let's say that hypothetically, the TL for CAP 29 set the following stat limits for the project.
PT: 150
ST: 155
PS: 100
SS: 250
BSR: 350
Under the old BSR calculator it would be possible to create the following Stat Spread and have it as legal within the limits.
91 HP / 52 Atk / 90 Def / 129 SpAtk / 90 SpDef / 108 Speed
PT: 144.465
ST: 147.194
PS: 87.694
SS: 245.211
BSR: 349.054
This spread may look familiar, and well, that's because it belongs to Keldeo, but with 20 Attack shaved off to force it into the limits. With its proper 72 Attack, Keldeo has a BSR of 371.169. Although it's perfectly possible that a TL would exclude this spread because of it being potential BSR abuse, it could theoretically slip through because it is somewhat below each of the proposed limits and isn't too far from some of our existing CAPs ie. Volkraken and Pajantom. In comparison, these two spreads reach BSR totals of 383.812 and 391.867 using the new BSR calculator.
With this in mind, it is clear that it is possible for TLs to set individually higher limits on certain stats with a lower BSR to encourage greater diversity, and avoid the problem of CAPs producing endless bulky attackers that reach the PT and ST limits and get close to either the PS or SS limit. Instead stat submitters will need to prioritise reaching individual limits that they deem important. For example Keldeo's spread would need to be modified to 80 / 48 / 80 / 129 / 80 / 108 for example, or to say 91 / 52 / 90 / 113 / 90 / 108.
To further illustrate this point, I refer back to the most recent stats stage for CAP 28. As mentioned previously a mask of 140 PS or SS was used to discourage optimised dump stats so as to allow for mixed spreads to have a reasonable chance to compete. As a reminder the limits for CAP 28 are also listed below.
PT: 120
ST: 180
PS: 220
SS: 225
BSR: 350
Minimum PS or SS: 140
The following chart displays what the selected spreads on the slate looked like with this mask added.

As you can see, with the mask applied most of the spreads hover approximately at the 330-340 BSR mark, with Quz and Jho's being the closest to the BSR limit of 350 at 347.161 and 344.794 respectively, and Pipotchi and Jas61292's the lowest at 331.124 and 309.511 respectively.
The next chart instead uses the new BSR calculation and allows for the real PS and SS values to be displayed.

Comparing this to the previous values, we can see a few notable differences. Overall the BSR on all of the spreads has lowered, although not proportionally. Jas61292's spread remains the lowest, but Jho's has now crept Quziel's to become the highest BSR. In addition Pipotchi's has overtaken Yay61's and Dogfish44's (rows 3 and 7) to enter the middle of the pack. The difference between Quziel and Jho's spread is also significantly higher than the 3rd place of Amamama's to be a difference of 11-15 instead of the original 2 point differential. Had this BSR calculator been implemented for the CAP 28 stat stage instead of the use of a mask, it is clear that a BSR limit of 330 would be more than sufficient to preserve the majority of these sets.
PT: 150
ST: 155
PS: 100
SS: 250
BSR: 350
Under the old BSR calculator it would be possible to create the following Stat Spread and have it as legal within the limits.
91 HP / 52 Atk / 90 Def / 129 SpAtk / 90 SpDef / 108 Speed
PT: 144.465
ST: 147.194
PS: 87.694
SS: 245.211
BSR: 349.054
This spread may look familiar, and well, that's because it belongs to Keldeo, but with 20 Attack shaved off to force it into the limits. With its proper 72 Attack, Keldeo has a BSR of 371.169. Although it's perfectly possible that a TL would exclude this spread because of it being potential BSR abuse, it could theoretically slip through because it is somewhat below each of the proposed limits and isn't too far from some of our existing CAPs ie. Volkraken and Pajantom. In comparison, these two spreads reach BSR totals of 383.812 and 391.867 using the new BSR calculator.
With this in mind, it is clear that it is possible for TLs to set individually higher limits on certain stats with a lower BSR to encourage greater diversity, and avoid the problem of CAPs producing endless bulky attackers that reach the PT and ST limits and get close to either the PS or SS limit. Instead stat submitters will need to prioritise reaching individual limits that they deem important. For example Keldeo's spread would need to be modified to 80 / 48 / 80 / 129 / 80 / 108 for example, or to say 91 / 52 / 90 / 113 / 90 / 108.
To further illustrate this point, I refer back to the most recent stats stage for CAP 28. As mentioned previously a mask of 140 PS or SS was used to discourage optimised dump stats so as to allow for mixed spreads to have a reasonable chance to compete. As a reminder the limits for CAP 28 are also listed below.
PT: 120
ST: 180
PS: 220
SS: 225
BSR: 350
Minimum PS or SS: 140
The following chart displays what the selected spreads on the slate looked like with this mask added.
As you can see, with the mask applied most of the spreads hover approximately at the 330-340 BSR mark, with Quz and Jho's being the closest to the BSR limit of 350 at 347.161 and 344.794 respectively, and Pipotchi and Jas61292's the lowest at 331.124 and 309.511 respectively.
The next chart instead uses the new BSR calculation and allows for the real PS and SS values to be displayed.
Comparing this to the previous values, we can see a few notable differences. Overall the BSR on all of the spreads has lowered, although not proportionally. Jas61292's spread remains the lowest, but Jho's has now crept Quziel's to become the highest BSR. In addition Pipotchi's has overtaken Yay61's and Dogfish44's (rows 3 and 7) to enter the middle of the pack. The difference between Quziel and Jho's spread is also significantly higher than the 3rd place of Amamama's to be a difference of 11-15 instead of the original 2 point differential. Had this BSR calculator been implemented for the CAP 28 stat stage instead of the use of a mask, it is clear that a BSR limit of 330 would be more than sufficient to preserve the majority of these sets.
I realise that this is a massive wall of text, and I hope it hasn't been too daunting to get through. To anyone that wants to have a play with the updated calculator you can find a link to it here, just make sure to make your own copy to edit. I would love to hear all of your thoughts about these changes and the spreadsheet itself. With any luck this will be fully operational for CAP 29.
Last edited: